来源:小编 更新:2024-12-15 01:18:03
用手机看

在数字货币的浪潮中,比特币作为首个成功的加密货币,其背后的技术支撑引起了广泛关注。其中,代数几何作为一种深奥的数学分支,与比特币的密码学基石紧密相连。本文将探讨代数几何在比特币中的应用,以及它如何为这一新兴领域提供坚实的数学保障。

代数几何起源于17世纪的欧洲,是数学中研究代数方程与几何图形之间关系的学科。它将代数与几何相结合,通过研究方程的解与几何图形的对应关系,揭示了数学世界的奇妙之处。代数几何的研究领域广泛,包括曲线、曲面、多面体等几何对象,以及它们与代数方程的关系。
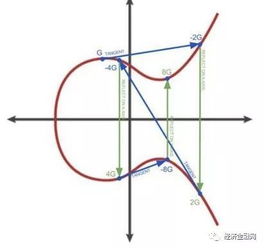
比特币的密码学基石之一是椭圆曲线密码学(ECC)。椭圆曲线是一种特殊的代数曲线,其数学性质为比特币提供了强大的安全性。在椭圆曲线密码学中,每个用户都有一个私钥和一个公钥。私钥是一个随机生成的数字,而公钥则是私钥通过椭圆曲线上的特定运算得到的。这种运算保证了公钥的唯一性和不可预测性。
代数几何在比特币中的应用主要体现在椭圆曲线密码学的实现上。以下是代数几何在比特币中的一些具体应用:
椭圆曲线上的点运算:比特币的公钥和私钥都是基于椭圆曲线上的点运算生成的。代数几何中的椭圆曲线方程为这些运算提供了理论基础。
数字签名:比特币的交易需要数字签名来验证交易的有效性。数字签名利用椭圆曲线密码学中的离散对数问题,通过代数几何中的数学原理实现。
密钥生成:比特币的密钥生成过程涉及到椭圆曲线上的随机数生成,这需要代数几何中的随机数生成算法。

代数几何在比特币中的应用,使得比特币的密码学安全性得到了极大的提升。以下是代数几何与比特币安全性的关系:
椭圆曲线密码学的安全性:椭圆曲线密码学基于椭圆曲线上的离散对数问题,而离散对数问题的困难性正是由代数几何中的椭圆曲线性质决定的。
抗量子计算攻击:随着量子计算的发展,传统的密码学算法面临着被量子计算机破解的风险。基于代数几何的椭圆曲线密码学具有较强的抗量子计算攻击能力。
数学证明的严谨性:代数几何为比特币的密码学提供了坚实的数学基础,使得比特币的安全性得到了数学证明的保障。
代数几何作为一门古老的数学分支,在比特币这一新兴领域找到了新的应用场景。通过椭圆曲线密码学,代数几何为比特币提供了强大的安全性保障。随着数字货币的不断发展,代数几何在密码学领域的应用将更加广泛,为数字世界的安全保驾护航。
